Prerequisites
- Segment Tree
- Depth First Search (DFS)
In this tutorial, we will learn how to preprocess a given tree to update a node and query in a subtree using a data structure like segment tree.
Definition: Subtree
A subtree of a tree T is a tree consisting of a node in T and all of its descendants in T.
We know there are well known data-structures to update and query in subarray of an array. We can use all of them to query in a subtree. Let's see how we'll do that!
Problem Setup
Suppose we have a tree with 7 nodes and the tree looks like the following:
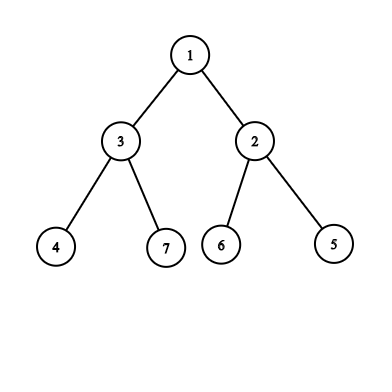
Example tree with 7 nodes showing the hierarchical structure
Let's assume there is a value written in every node. For example, the numbers are as following:
| Node Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Assigned Value | 9 | 10 | 11 | 6 | 8 | 12 | 5 |
The Challenge
For example, a tree having node 2 as root is the subtree of the mentioned tree.
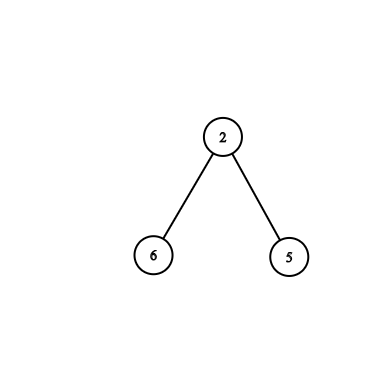
Subtree rooted at node 2, containing nodes 2, 5, and 6
So, for an example, if we want to get the maximum value among that subtree, we need to find the maximum value among the nodes 2, 6 and 5.
| Node Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Assigned Value | 9 | 10 | 11 | 6 | 8 | 12 | 5 |
The Solution: DFS Preprocessing
But there is a solution! Let's traverse the tree by DFS fashion and write the traversal order on these nodes.
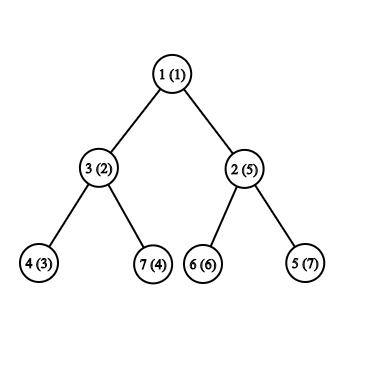
Tree with DFS traversal order marked on each node
DFS Traversal Result:
| Traversal Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Node Number | 1 | 3 | 4 | 7 | 2 | 6 | 5 |
| Assigned Value | 9 | 11 | 6 | 5 | 10 | 12 | 8 |
Now back to the query part, the candidate nodes of the query are highlighted as follows:
| Traversal Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Node Number | 1 | 3 | 4 | 7 | 2 | 6 | 5 |
| Assigned Value | 9 | 11 | 6 | 5 | 10 | 12 | 8 |
Formula and Implementation
Range Formula for Subtree:
Explanation:
If we go back to our example subtree, the left traversal order of the highlighted segment is 5, which is the traversal order of node 2, which is the root of the subtree. The right traversal order will be the last node of that subtree, which can be easily found by adding subtree size.
DFS Implementation:
How we can traverse the tree in DFS fashion and find subtree size:
int traversalOrder = 0;
int sz[Max];
int order[Max];
vector<int> adj[Max];
int dfs(int u) {
order[u] = ++traversalOrder;
sz[u] = 1;
for(int v : adj[u]) {
if (!order[v]) {
sz[u] += dfs(v);
}
}
return sz[u];
}Range Query Function:
Getting traversal order range for a subtree:
pair<int, int> getRange(int root) {
int rootTraversalOrder = order[root];
int l = rootTraversalOrder;
int r = rootTraversalOrder + sz[root] - 1;
return {l, r};
}Applications
Subtree Sum Queries
Calculate sum of all values in a subtree efficiently
Subtree Maximum/Minimum
Find maximum or minimum value in any subtree
Subtree Updates
Update all nodes in a subtree with range update operations
Complex Queries
Any query that can be answered on arrays can now work on subtrees
Complexity Analysis
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| DFS Preprocessing | O(n) | O(n) |
| Range Calculation | O(1) | O(1) |
| Subtree Query (with Segment Tree) | O(log n) | O(n) |
| Subtree Update (with Segment Tree) | O(log n) | O(n) |
Key Takeaways
DFS Preprocessing
Convert tree structure to array indices using DFS traversal
Subtree to Range
Map subtree operations to contiguous array range operations
Efficient Queries
Use any array data structure (Segment Tree, Fenwick Tree) on trees
Versatile Technique
Works with any associative operation (sum, max, min, XOR, etc.)
Conclusion
Now we can update a node and query over a subtree using a data structure like segment tree. This technique is fundamental for solving complex tree-based problems efficiently.
Thank you for reading! 😊